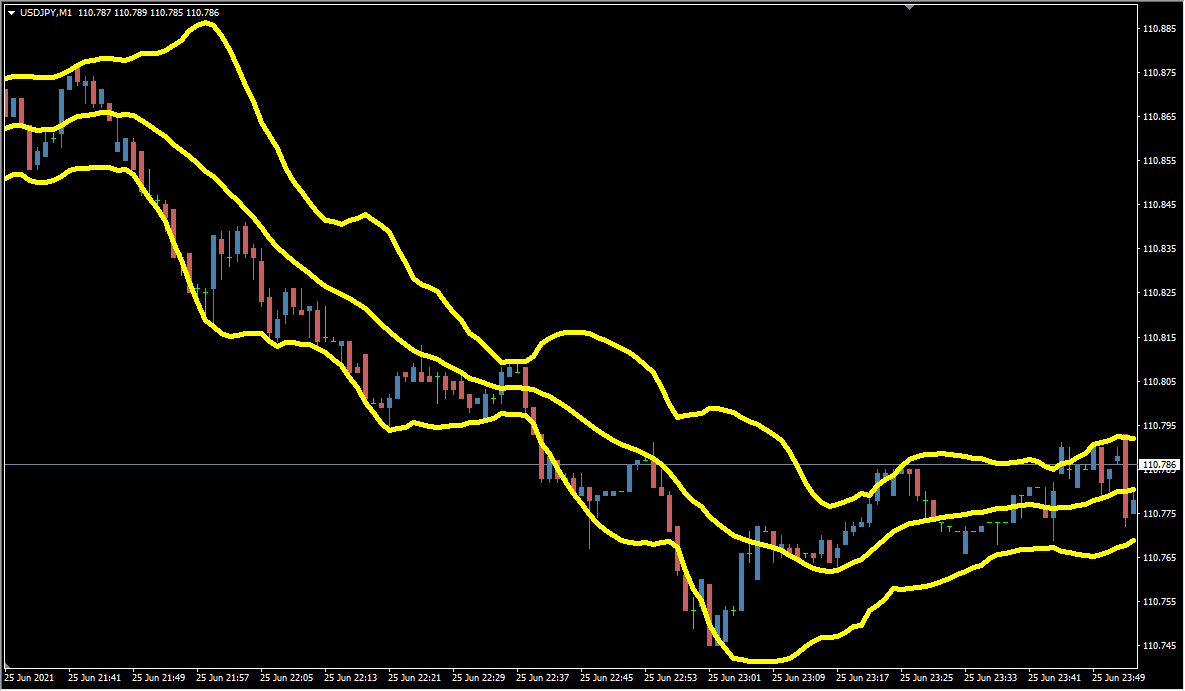
ボリンジャーバンドは、ジョン・ボリンジャー氏が開発した価格エンベロープの一種で、価格が安いか低いかを相対的に見分けるのに適しています。
非常に人気のあるテクニカル指標で、商標登録もされているので正しくは『ボリンジャーバンド®』と記載します。
単純移動平均（SMA）を中心におき、その上下に2本のバンドを表示するエンベロープの一種で、バンドの距離は標準偏差に基づいているため、価格のボラティリティーの変動に合わせて調整されます。
単独で使われることは推奨されておらず、水平線やプライスアクション、フィボナッチなどと組み合わせることが多いテクニカルです。
ボリンジャーバンドの計算式
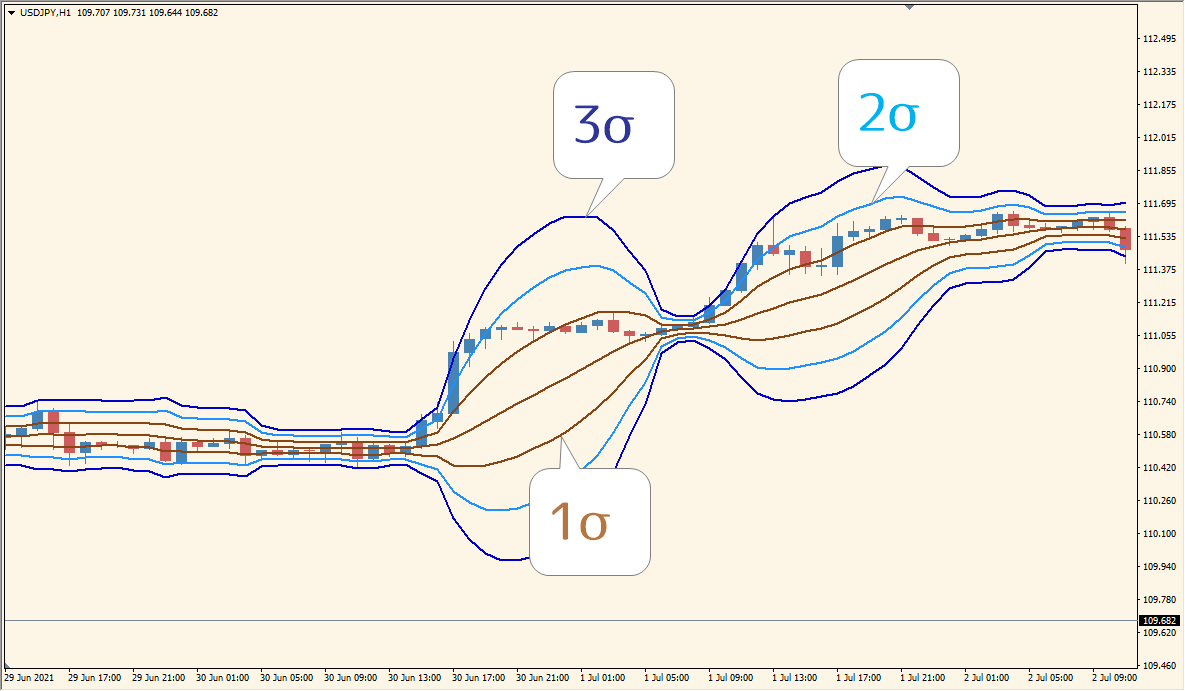
標準偏差はシグマ（σ）で表し、一般的には1σ，2σ，3σの3種類がよく使われます。
・標準偏差の計算式
標準偏差 ＝ √(n×n日間の終値の2乗の合計 － n日間の終値の合計の2乗) ÷ (n×(n－1))
・ボリンジャーバンドの計算式
±1σ ＝ n日の移動平均 ± n日の標準偏差
±2σ ＝ n日の移動平均 ± n日の標準偏差 × 2
±3σ ＝ n日の移動平均 ± n日の標準偏差 × 3
実際に計算してみると・・・
ここでは実際にボリンジャーバンドの計算をおこなってみましょう。
まず計算をシンプルにするために、5本のローソク足期間のボリンジャーバンドを計算しましょう。
直近5期間の終値が25.5、26.75、27.0、26.5、27.25だったと仮定します。
まず最初に中心のラインである単純移動平均を計算します。
25.5 + 26.75 + 27.0 + 26.5 + 27.25 = 133.0
133.0 / 5 = 26.6
次に、各ローソク足終値から26.6を引き、この値を平方します。
25.5 – 26.6 = -1.1の2乗 = 1.21
26.75 – 26.6 = 0.15の2乗 = 0.023
27.0 – 26.6 = 0.4の二乗 = 0.16
26.5 – 26.6 = 0.1の二乗 = 0.01
27.25 – 26.6 = 0.65の2乗 = 0.423
上記の計算値を足して5で割り、この値の平方根を求めて標準偏差を算出します。
1.21 + 0.023 + 0.16 + 0.01 + 0.423 = 1.826
1.826 / 5 = 0.365
0.365の平方根＝0.604（標準偏差）
よって、
ボリンジャーバンドの上限は、26.6 + 0.604 = 27.204となります。
ボリンジャーバンドの中段は、26.6（単純移動平均線）となります。
ボリンジャーバンドの下限は、26.6 – 0.604 = 25.996 となります。
ボリンジャーバンドの上限は、26.6 + (2 × 0.604) = 27.808となります。
ボリンジャーバンドの中段は、26.6（単純移動平均線）となります。
ボリンジャーバンドの下限は、26.6 – (2 × 0.604) = 25.392 となります。
ボリンジャーバンドの使い方
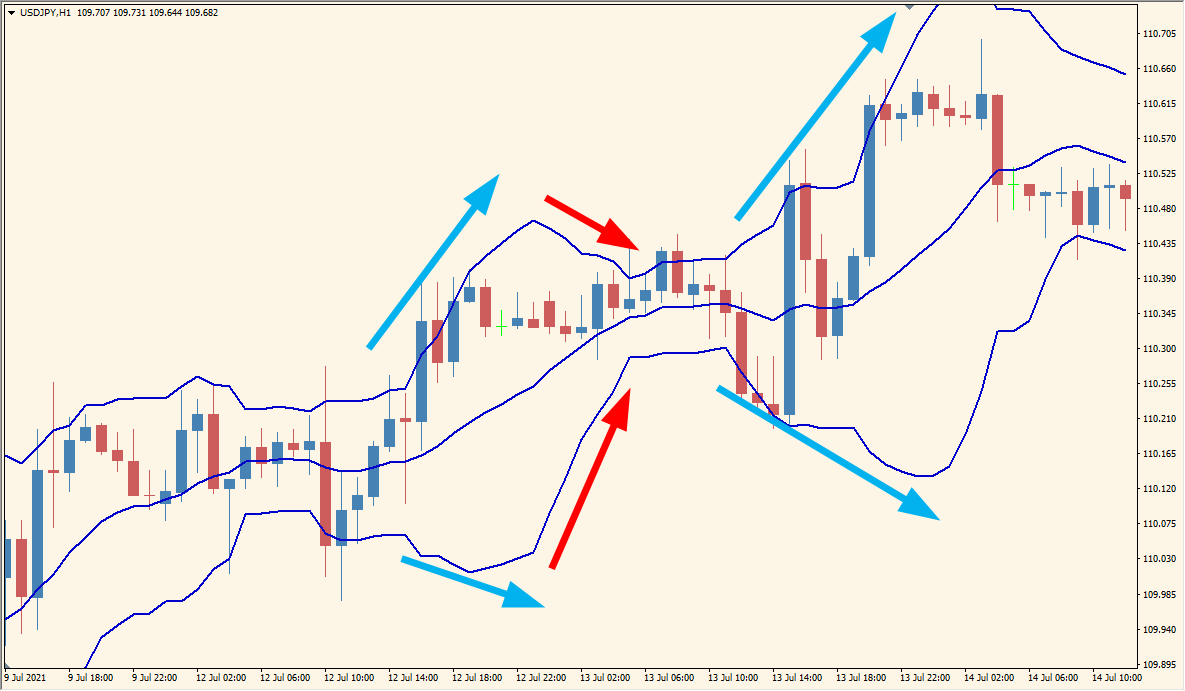
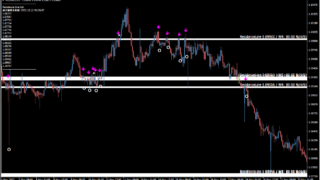
まず基本的な使い方としては、相場の勢いを見る時に使います。
上記の青矢印の箇所はバンドが拡大（エクスパンション）、赤い部分は収縮（スクイーズ）しているところです。
相場は拡大と収縮を繰り返しますが、ボリンジャーバンドの拡大中は相場が強いトレンド状態ということを表します。
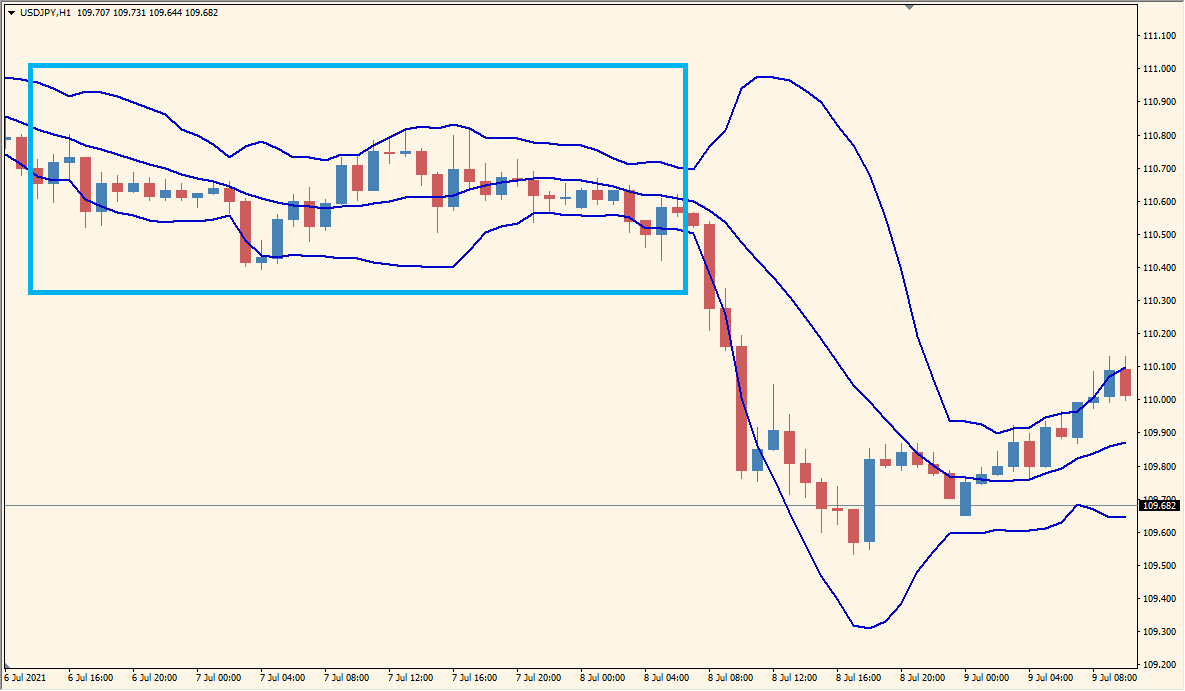
逆に上記のように、収縮（スクイーズ）が続いている時はトレードには向きませんが、スクイーズが長くなればなるほど、エネルギーが溜まり、大きな拡大の前触れでもあります。
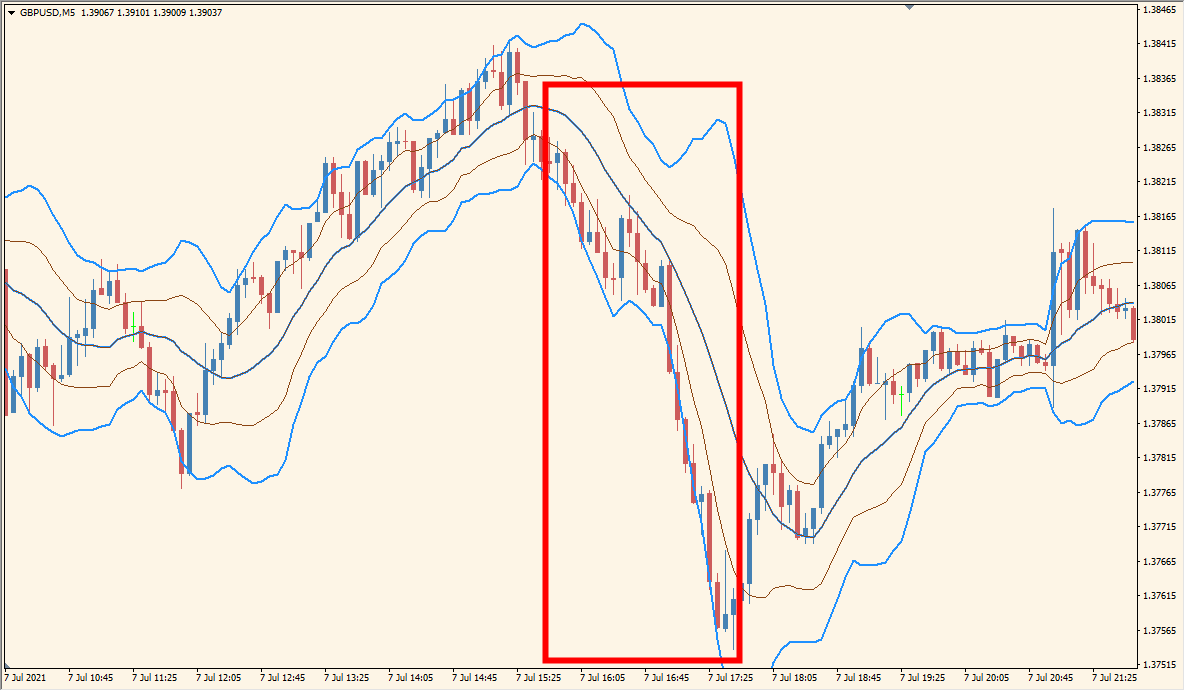そしてもう一つ、ボリンジャーバンドの特徴的な動きとしてバンドウォークがあります。
バンドウォークは、エクスパンションを伴ってローソク足が2シグマに沿って上昇または下降していくことで、勢いのあるトレンドの時に発生します。
バンドウォークが発生した場合は、基本的には1σの中に戻ってくるまではがっちりホールドです。
価格がバンド内に収まる確率について
ボリンジャーバンドを統計的に考えると、ローソクが各シグマ内に収まる確率は下記の数値になります。
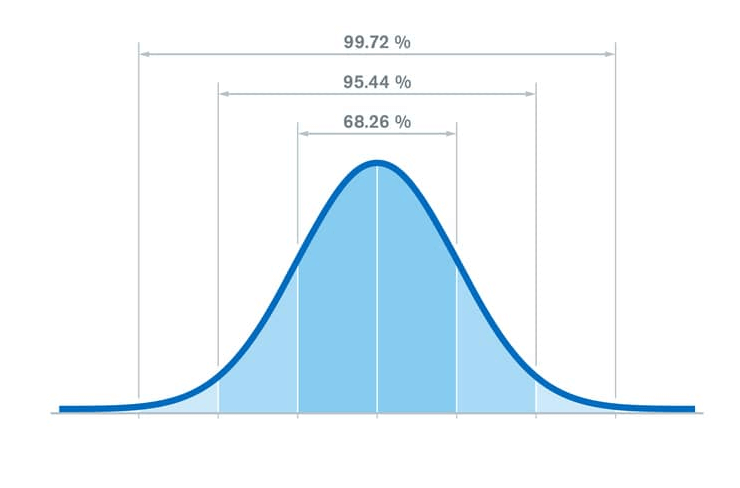
ボリンジャーバンドの±1σの範囲内に収まる確率 ⇒ 約68.26％
ボリンジャーバンドの±2σの範囲内に収まる確率 ⇒ 約95.44％
ボリンジャーバンドの±3σの範囲内に収まる確率 ⇒ 約99.72％
つまり2σから外に価格がいる状況は全体の4.56％しかないので、2σ突破したところで逆張りでエントリーしておけばほぼ勝てるというわけです。
しかし実際ボリンジャーバンドを逆張りで使うとあまり勝てないということはよく知られています。
開発者のジョン・ボリンジャー氏も基本的にはボリンジャーバンドを逆張りには使わず、順張りで使うことを推奨しています。これはなぜなのでしょうか？
ボリンジャーバンドの問題点
開発者のジョン・ボリンジャー氏
実はボリンジャーバンドで取り扱うことができるデータの条件は限定されております。
まずボリンジャーバンドを統計的に見ると、平均に対してプラスマイナス1σの間に収まる確率が約68％、2σ内は95.4%、3σ内は99.7%となり、非常に有用なテクニカル指標に思えますが、実際に使ってみるとこの確率には収まらないとは多くの人が気づいているところかと思います。
この原因はボリンジャーバンドで扱っている価格が「正規分布」していないデータであるということが原因です。
正規分布しているデータとは、動きがランダムであり、規則がなく、平均的に散らばっていることが条件なのですが、我々が利用する「価格」にはモメンタム（勢い）がありますので実は正規分布しておらず、ボリンジャーバンドでの分析には向かないデータです。
この問題点に関しては下記のサイトが詳しく解説してくれています。テクニカル指標を使ってトレードを行う上で非常に大切なことですのでしっかり理解してくださいね。
参照リンク：トレードで負けている人は正規分布していないデータを使っている
